Articles
Something has happened to my data: potential problems with standard normal variate and multiplicative scatter correction spectral pre-treatments
This column has been developed from two recent publications by Tom Fearn. "The effect of spectral pre-treatments on interpretation” and "On the geometry of SNV and MSC"
And now for something completely different!
This column is about “Computational Chemistry”.
The definition of Chemometrics is: “The application of mathematical and statistical techniques to extract information from complex data”. You might think that it is computational chemistry, but I suspect that the majority of people who use computational chemistry have little knowledge or interest in chemometrics and similarly most chemometricians have little interest in computational chemistry. Computational chemistry uses the results of theoretical chemistry, incorporated into efficient computer programs, to calculate the structures and properties of molecules and solids. It seems that these two topics are conducted by two groups on parallel tracks, which, of course, never meet. This could be a mistake.
Shedding light on evidence: forensic applications of UV/visible spectroscopy
This short review shows that UV/visible spectroscopy plays a key role in the discrimination of colour in the forensic analysis of fibres and inks. The application of chemometrics, however, is vital in many cases to enhance such discrimination and to put it on a quantitative basis so providing objective justification for the conclusions of the analyst.
Back to basics: multivariate qualitative analysis, SIMCA
In our previous column we introduced CVA, one of the very early applications of multivariate analysis (1930s). In this column we will discuss SIMCA (officially it is Soft Independent Modelling of Class Analogies, but no one uses the long form!). SIMCA was invented 30 years later by another pioneer, Svante Wold (the man who coined the word “chemometrics”).
Back to basics: multivariate qualitative analysis, canonical variates analysis
A.M.C. Daviesa and Tom Fearnb
aNorwich Near Infrared Consultancy, 75 Intwood Road, Cringleford, Norwich NR4 6AA, UK. E-mail: [email protected]
bDepartment of Statistical Science, University College London, Gower Street, London WC1E 6BT, UK. E-mail: [email protected]
Back to basics: qualitative analysis, introduction
A.M.C. Davies and Tom Fearn
Norwich Near Infrared Consultancy, 75 Intwood Road, Cringleford, Norwich NR4 6AA, UK. E-mail: [email protected]
Department of Statistical Science, University College London, Gower Street, London WC1E 6BT, UK. E-mail: [email protected]
Back to basics: the "final" calibration
The starting point for this column is the last one from last year! In that column TD began what was intended to be a two-part story but has, with this column, become a story in four parts. There were required topics we had not covered and we need to begin this column by completing the discussion of removing multiplicative effects by describing what the two most popular methods do to NIR spectra.
Back to basics: removing multiplicative effects (1)
The last TD column showed the effect of calculating second derivatives on a set of 100 spectra, which will be the starting point for this column.
Back to basics: spectral pre-treatments, derivatives
This column is about the most basic of pre-treatments, which has been used in spectroscopy well before the word "Chemometrics" was invented.
Back to basics: running your first PLS calibration
A.M.C. Davies
Norwich Near Infrared Consultancy, 75 Intwood Road, Cringleford, Norwich NR4 6AA, UK. [email protected]
An evergreen problem in multivariate calibration
N.M. Faber,a,* and R. Rajkób
aChemometric Consultant, Rubensstraat 7, 6717 VD Ede, The Netherlands. [email protected]
bDepartment of Unit Operations and Food Engineering, Szeged College of Food Engineering, University of Szeged, H-6701 Szeged, POB 433, Hungary
Back to basics: preparing for PLS calibration
A.M.C. Davies
Norwich Near Infrared Consultancy, 75 Intwood Road, Cringleford, Norwich NR4 6AA, UK
Back to basics: calibration statistics
A.M.C. Daviesa and Tom Fearnb
aNorwich Near Infrared Consultancy, 75 Intwood Road, Cringleford, Norwich NR4 6AA, UK
bDepartment of Statistical Science, University College London, Gower Street, London, UK
Back to basics: observing PLS
A.M.C. Daviesa and Tom Fearnb
aNorwich Near Infrared Consultancy, 75 Intwood Road, Cringleford, Norwich NR4 6AA, UK
bDepartment of Statistical Science, University College London, Gower Street, London, UK
Back to basics: when you need more than Principal Component Analysis
A.M.C. Daviesa and Tom Fearnb
aNorwich Near Infrared Consultancy, 75 Intwood Road, Cringleford, Norwich NR4 6AA, UK
bDepartment of Statistical Science, University College London, Gower Street, London, UK
Back to basics: applications of principal component analysis
A.M.C. Davies
Norwich Near Infrared Consultancy, 75 Intwood Road, Cringleford, Norwich NR4 6AA, UK
Back to the future: total spectroscopic laboratory informatics
Tony Davies
External Professor, University of Glamorgan, UK, c/o Waters Informatics, Europaallee 27–29, 50226 Frechen, Germany
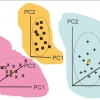
Back to basics: the principles of principal component analysis
PCA is a mathematical method of reorganising information in a data set of samples. It can be used when the set contains information from only a few variables but it becomes more useful when there are large numbers of variables, as in spectroscopic data.
Independence rules (or Rules for independence)
A.M.C. Davies
Norwich Near Infrared Consultancy, 75 Intwood Road, Cringleford, Norwich NR4 6AA, UK
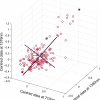
Estimation of prediction uncertainty for a multivariate calibration model
The goal of building a multivariate calibration model is to predict a chemical or physical property from a set of predictor variables, e.g. analyte concentration or octane number from a near infrared (NIR) spectrum. A good multivariate calibration model should be able to replace the laborious, possibly imprecise reference method. The quality of a model therefore primarily depends on its predictive ability. Other properties such as interpretability of the model coefficients might also be of interest, but here the focus is on the problem of quantifying the predictive ability.